The result seems to me to be more like Reverb in my perception/use. Where the lower it is (like R= 0.5), the more restricted the space is so it bounces around more/intimate and the higher values are more like the room is expanding so its not as bouncy.
What does R refer to or what is it a spectrum from->to? What does the absence and abundance of resonance reify as observably?
So, this won’t be the most scientifically accurate description of what’s going on, and my own understanding and word usage may be imperfect, but hopefully it gives you at least some idea of what’s happening.
With your low-pass filter you’re making your signal reject frequencies any higher than the cutoff point that you have set. All it does is eliminate those higher frequencies without modifying anything about the frequencies lower than, or at your cutoff point.
When you begin to add resonance, what you’re doing is accentuating the frequency that your cutoff point is set to. So not only are you rejecting the frequencies higher than your cutoff point, you are making the frequency at the cutoff more prominent in your remaining signal. The frequencies below the cutoff point will remain unaltered other than at a lower resonance value you will see a bit of emphasis at frequencies immediately below the cutoff frequency as the signal is drawing those frequencies up sympathetically with the boosted resonance frequency. As you increase the resonance you are further accentuating the frequency at the cutoff point to where the signal will show more of a spike at the cutoff frequency rather than the slight rise seen at lower resonance values. This narrows the band of any sympathetic frequencies that may have been previously affected at lower resonance values. While the lower frequencies are still present and unaltered in your signal since they are below the cutoff, the prominence of the frequency at the cutoff point is being amplified so drastically in comparison that your signal is dominated by the resonated frequency.
I hope this makes sense. I found it difficult to know if I was saying things in as clear a way as needed.
And to amend something above. The band of frequencies doesn’t narrow per se as you increase the resonance, but the band of frequencies affected by increased resonance can be adjusted (narrowed or widened) in many filters. You’ll typically see this referred to as the Q factor of the resonated signal.
Is there a song that exemplifies what you’ve described so I can contextualize/see it in action in a palpable way?
Any techno track from the 90s that used a Roland TB303 synth used this effect to the maximum
The 303 is famous for it
A lot of times when learning about synthesis it can be more useful to have a visual guide as to what’s happening to your signal. Instead of a song have a look at this video. The first 5 minutes goes over what I’d gone over in my first post, and he goes on a bit about a few other things after that. Give it a look.
Are you into audio production at all? You could get any soft synth and experience it for yourself. Vital is free on desktop or various options on mobile.
The result seems to me to be more like Reverb in my perception/use.
You’re on to something: reverbs often intentionally create resonances. Reverbs can be simulated with a filter (although commercial reverb plugins and hardware typically sprinkle in some non-linear goodness).
What does the absence and abundance of resonance reify as observably?
In audio systems, it sounds like you added ringing to the signal. If it’s too much ringing, eventually the ringing will dominate over your signal and you’ll basically get a sine wave at the resonant frequency.
Below is a response of a filter with a resonance:
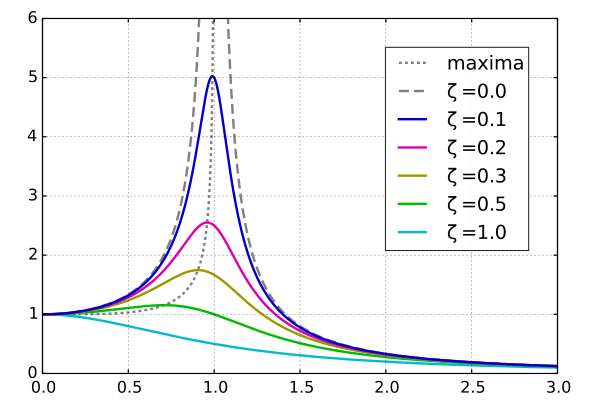
You’d have to show me a diagram or plugin with the control labeled “R” to be sure, but I believe that with respect to the above diagram, R is equivalent to ζ (zeta). However, some plugins use Q = 1/(2ζ) as the parameter for the user to change, in which case the intuition is practically “backwards”.
When ζ is about 1, the system described by the graph basically doesn’t ring. As ζ goes to 0, the resonant frequency and its neighbors start to get boosted, giving the characteristic “ringing” sound. If ζ = 0 (or practically is close enough), you get an oscillator, i.e. you generate a sine wave with the resonant frequency.
What does R refer to or what is it a spectrum from->to?
The spectrum of the filter is actually the curve above, along with its phase curve, which gives you the output of the resonant filter given any input. ζ and Q are different ways of specifying the strength of the resonance.
Note that I used a filter with just a resonance for simplicity, but any filter can have a resonance, including low-pass filters, in which case ζ is often used as a parameter in the math. You can logically think of a resonant low pass filter as a “non-resonant” low pass in cascade with a resonant peak (order doesn’t matter) at the same frequency you set the low pass to, even though they’re not designed that way.
IIRC resonance happens when the filter has a quality Q >1. The cutoff frequency gets amplified, the higher ones get attenuated.
What is Q?
Also, Is there a good song that exemplifies what this sounds like? Like what would stylistically motivate an artist to integrate one?
What is Q?
The quality of the resonator.
Read here https://en.m.wikipedia.org/wiki/Q_factor
Like what would stylistically motivate an artist to integrate one?
I don’t think they are used for music.
Basically anything that affects waves is used for music.
Wah-wah pedals are resonant filters with an adjustable cut off. Rock and metal guitarists have been using them in solos to create that expressive “crying guitar” sound. Classic example is the solo in Sweet Child O’Mine by Guns N’ Roses.
What’s the context for your question? My first thought when seeing your post was synthesizers.
deleted by creator




